- Discrete rate of return over the period t,
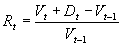
- Continuously compounded rate of return,
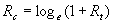
CURTIN UNIVERSITY OF TECHNOLOGY
CURTIN BUSINESS SCHOOL
School of Economics and Finance
FINANCE (PORTFOLIO MANAGEMENT) 301
SEMESTER1, 1998
ASSIGNMENT
Prepared For : Dr. Lakshman Alles
Prepared By : Herlini Suwarko, Carol Chan Poh Har & Chow Tai Wei, David
Table of Content
1 Introduction
*2. Organisation Analysis
*2.1 Broken Hill Proprietary Limited
*2.2 The News Corporation Limited
*2.3 Coles Myers Limited
*3. Risk Return Characteristics Analysis *
3.1 Risk Return Analysis of Each Stock and the Index
*3.2 Covariance & Correlation Coefficients between Each Pair of Stocks and with the Market Index *
3.3 Stocks and Market Analysis
*4. Equally Weighted Portfolio *
4.1 Weighted Average Rate of Return
*4.2 Comparison between Equally Weighted Portfolio and Individual Stocks
*5. Markowitz Tangent Portfolio *
5.1 Determining the Proxy for Risk-free rate
*5.2 Weights of the Markowitz Tangent Portfolio
*6. RISK *
6.1 Systematic Risk & Unsystematic Risk
*6.2 Partitioning the Total Risk
*7. BIBLIOGRAPHY *
8. APPENDICES
1. Introduction
This report attempts to illustrate the relationship between risk and rate of return of an individual stock compared with both an equally weighted and a Markowitz tangent portfolio of 3 selected stocks. The systematic and unsystematic risk components of each stock and of the portfolio are examined.
The common stocks of The Broken Hill Proprietary Company Limited (BHP), Coles Myers Limited (CML), and The News Corporation Limited (NCP), together with the All Ordinaries Accumulation Index were chosen to illustrate the above. Their Friday closing prices / index, 90-days bill rate, dividend payment and market information were compiled from past issues of The Australian Financial Review, from 12 September 1997 till 15 March 1998, and the AFR web site at http://www.tradingroom.com.au/investments; while the company information were gathered from their respective web sites and other sources.
In preparing this report, we utilised the electronic spreadsheet Excel 97 in computing the results of which the summary is presented here. The detailed calculations on the work sheets can be found in the appendices that follow. We have made the assumptions that all dividend payments were withdrawn in the same period as they were paid (ie. they are not reinvested), and were reflected in the Friday’s price for calculation of its returns.
2.1 Broken Hill Proprietary Limited
The Broken Hill Proprietary Company Limited (BHP) is Australia’s largest public company. BHP was incorporated in Melbourne in 1885, and began operation as a miner for silver, lead and zinc at Broken Hill in NSW.
Today, BHP is a leading global resources company with operations and offices in 70 countries. The group will remain a diversified but more focused resource company. It comprises four main business groups: BHP Copper, BHP Minerals, BHP Steel and BHP Petroleum. In addition, the BHP service companies group incorporates service and specialist operations including BHP Engineering, BHP Information Technology, BHP Insurance, BHP Power and BHP Transport.
In all its operations, BHP aims to contribute to growth and improve living standards. It is also continuing to diversify its product range and markets, and to maintain its position as a low cost, high quality producer.
2.2 The News Corporation Limited
The News Corporation Limited (NCP) is a leader in the global media and entertainment industry. They continue their focus on Children’s and news programs and took major steps to strengthen future position.
Fox Kids Worldwide joint venture with Saban Entertainment, announcing the acquisition of international family entertainment. The expansion has resulted in the Company having either full or partial ownership positions in more than 90 channels worldwide. This makes News Corporation the largest TV network operator in the world.
In Australia, the Company is taking steps to rationalise the very competitive pay television market. The company looks forward to a rapid acceleration of its global growth strategy. The next revolution in the media industry is the Digital Information age. It changes the way content is created by replacing it with electronic distribution to a global market. Print remains a very good business for News Corporation and the Company will continue to prosper in it.
Coles Myers Limited (CML) is Australasia’s leading retail organisation with head office based in Melbourne. It is also among the top twenty retailers in the world. The Company, which is Australia’s largest non-government employer, operates a range of retail businesses in both Australia and New Zealand. Its business coverage includes Premium and discount supermarkets, department stores, discount stores and speciality operations.
The CML groups owns the following businesses: Bi-Lo, Coles, Coles Myers Properties, Fosseys, Katies, K-mart, Liquorland, Officeworks, Red Rooster, Targets and World 4 Kids. It operates over 1800 stores throughout Australia and New Zealand.
The economic outlook indicates low retail growth. The Company aims to maintain sales growth above industry forecasts by focusing on improving retail performance and capital investment. Coles Myers will also focus on reducing costs, especially at World 4 Kids.
3. Risk Return Characteristics Analysis
3.1 Risk Return Analysis of Each Stock and the Index
Both types of returns were calculated as follow:
The following charts illustrate the performances of the individual stocks and the market over the sample period.
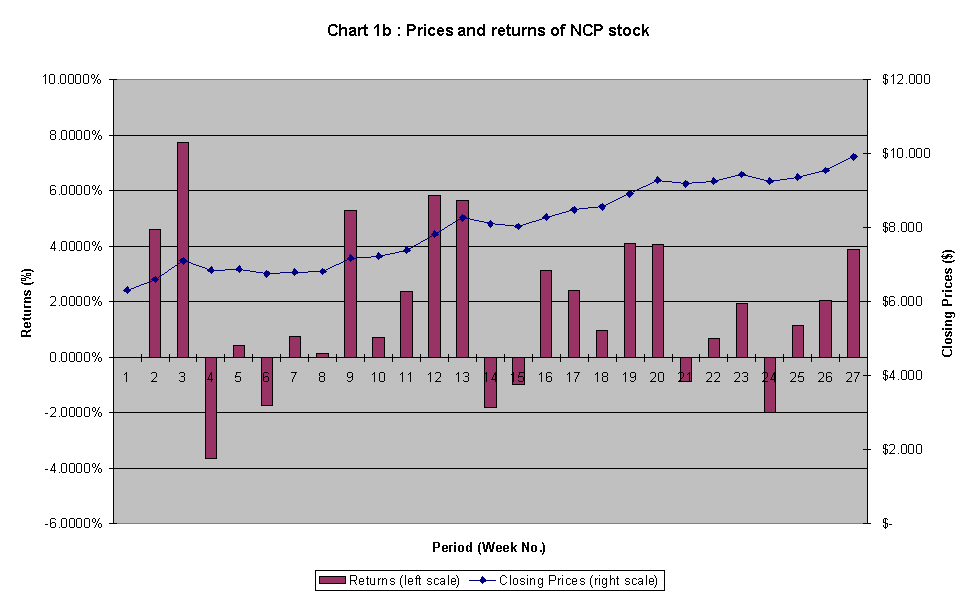
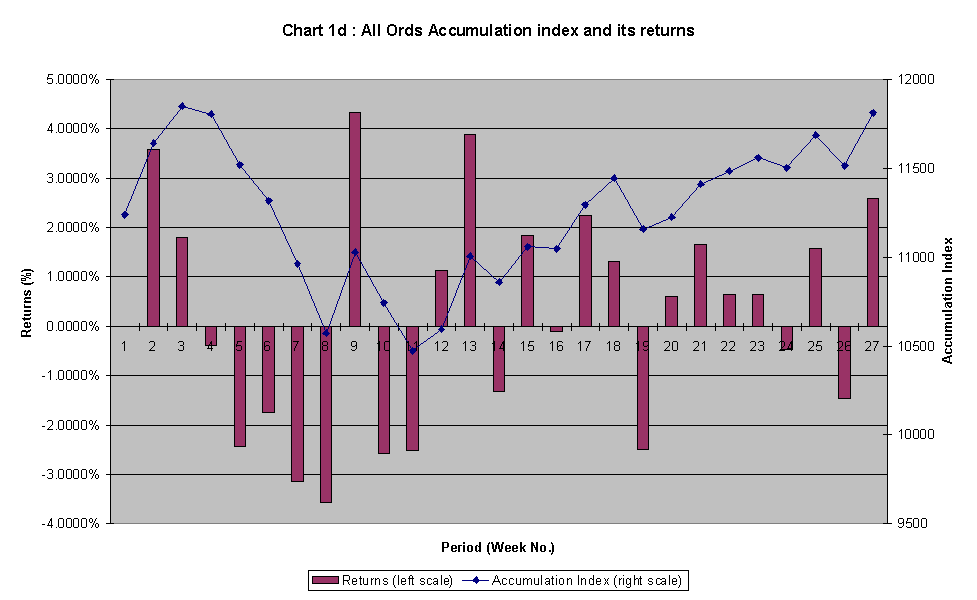
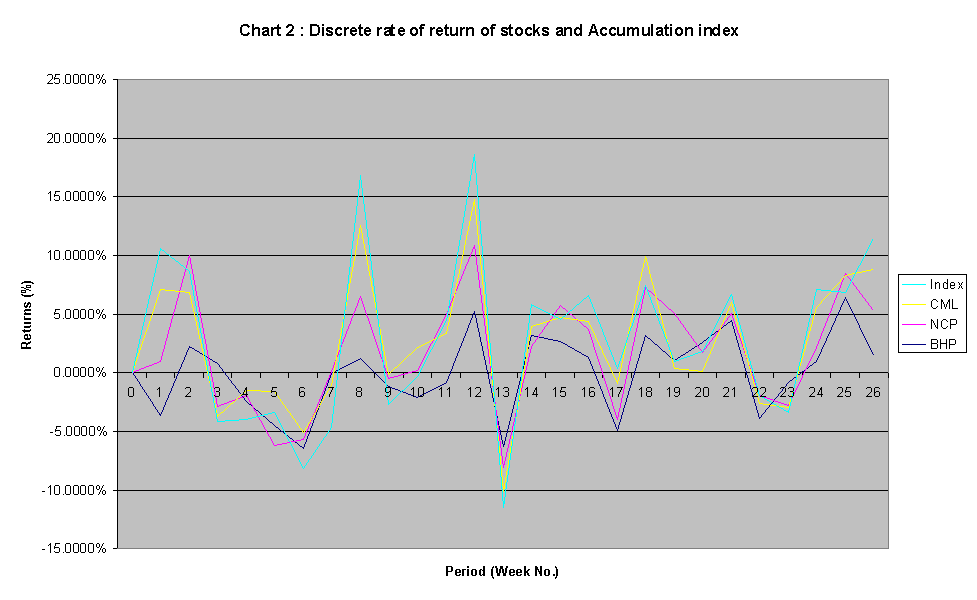
Graphing their discrete returns together, it seems that the movement of the returns of the stocks moves closely with the market index:
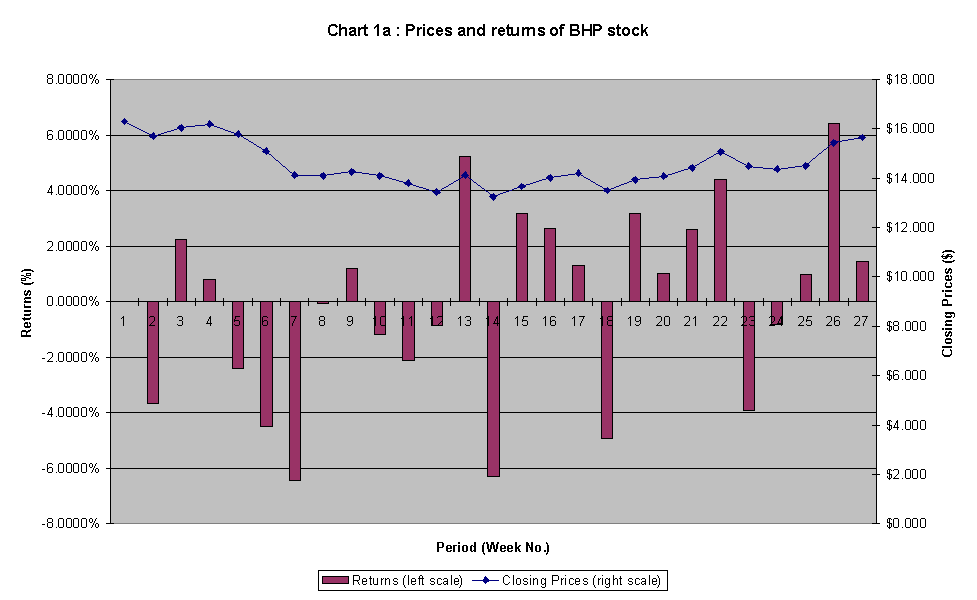
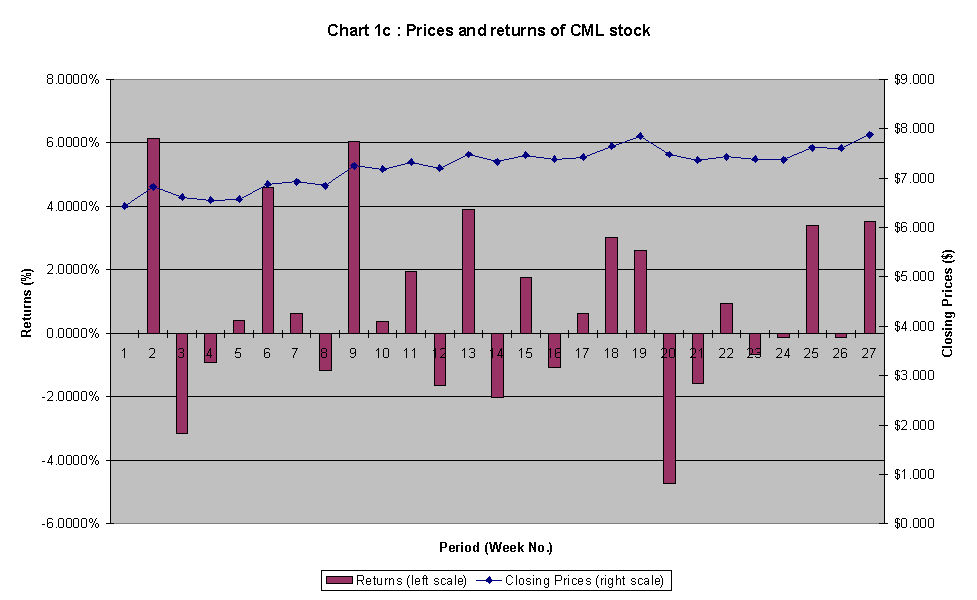
Referring to chart 1a to chart 1d, the length of maroon column of each stock / index represents the variability of their weekly returns. As illustrated, the aggregated return of the market index seems to fluctuate the least (between 4.3239% and –3.5737%), larger fluctuation by CML (between 6.1431% and –4.7134%), then NCP (7.7273% and –3.6568%), while return of BHP fluctuates the most (between 6.4138% and –6.4319%). (This observation is in line with the ranking of the magnitude of standard deviations for the stocks and index that follows.)
The arithmetic and geometric mean figures, variances and subsequently the standard deviations of returns of the 3 stocks and the market index were worked out in Appendix 2.
They were computed using the formulas below:
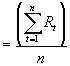
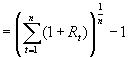
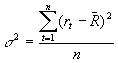
A summary of the results were presented in the table below:
BHP |
NCP |
CML |
All Ords Accum Index |
|||||
Discrete |
Continuous |
Discrete |
Continuous |
Discrete |
Continuous |
Discrete |
Continuous |
|
Arithmetic Mean |
-0.0271% |
-0.0856% |
1.7942% |
1.7418% |
0.8725% |
0.8339% |
0.2163% |
0.1915% |
Geometric Mean |
-0.0855% |
-0.1447% |
1.7570% |
1.7060% |
0.8373% |
0.7994% |
0.1917% |
0.1670% |
Variance |
12.0756% |
12.1987% |
7.8778% |
7.5864% |
7.3857% |
7.2325% |
5.1296% |
5.1092% |
Standard deviation |
3.4750% |
3.4927% |
2.8067% |
2.7543% |
2.7177% |
2.6893% |
2.2649% |
2.2604% |
Table 1 : Risk and Return of each stock and the market
The BHP stock bears the highest risk, followed by NCP’s. CML’s stock is the least risky of the three (indicated by their standard deviations). Their risks are however, higher than the market risk (represented by the s of the All Ords Accumulation Index).
NCP offers the highest return (at s = 2.8067%), followed by CML (at s = 2.7177%). BHP offers the lowest return (and the highest s = 3.4750%), which is even lower than the market return (at s = 2.2649%).
The risk-return relationships of every individual stock and the market index are collated in Chart 3 below:
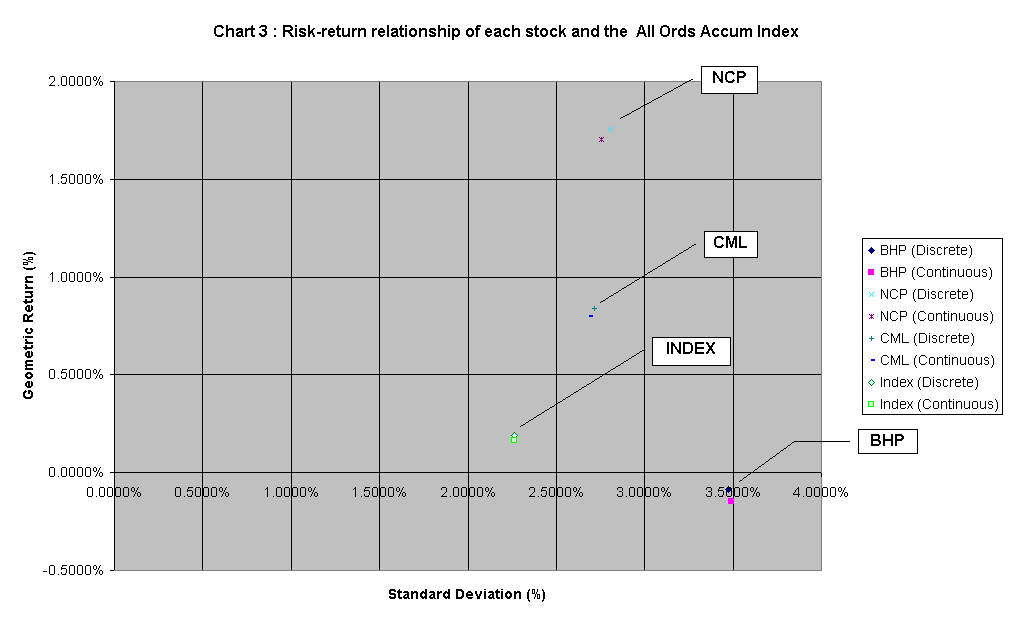
From the above chart, it seems that BHP is the worst of the 3 stocks as it bears the highest risk with the lowest return. Investors may favour NCP over CML as it offers higher return over CML’s at around the same risk level.
The market index (as a proxy for a diversified portfolio of about 250 stocks in listed in ASX) demonstrates the "power" of diversification by exhibiting the lowest risk, but also the lowest return.
Chart 4 below shows the growth in relative prices of each stock and the market with respect to a base value of 100 at period 0. It illustrates the instantaneous geometric mean return over the 26 weeks’ period, and the ranking of the return at the 26th week is the same as the geometric mean return ranking featured in table 1.
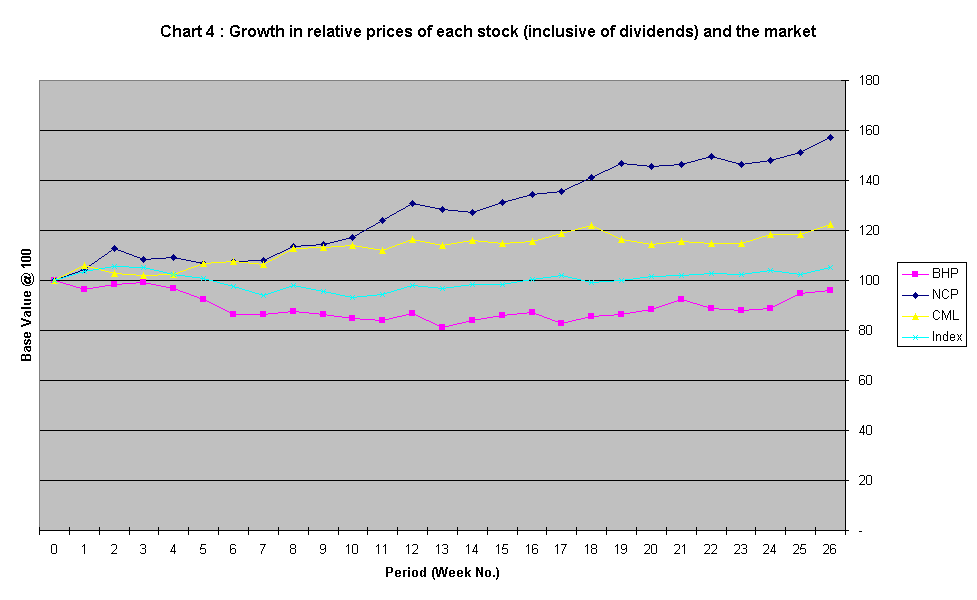
The conversion of stock prices and the indices to reference at base value of 100 is made possible by multiplying the prices / indices by their respectively factors which turn period 0 to 100. Also, dividends were added to back to their respectively share prices for the period they are paid. This is a better and more appropriate comparison as the returns were calculated this way, and the fact that the All Ords accumulation index takes into account of the accumulated market value plus dividends.
3.2 Covariance & Correlation Coefficients between Each
Pair of Stocks and with the Market Index
The covariances and the correlation coefficients between each pair amongst the 3 stocks, and between each stock and the market index were calculated using the formulas below:
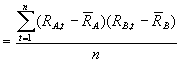
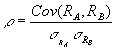
Using Excel 97, we obtained the following results of calculation:
Discrete Return |
Continuous Return |
|||
Covariance |
Correlation Coefficient |
Covariance |
Correlation Coefficient |
|
| BHP / NCP | 2.7621 |
0.2832 |
2.7280 |
0.2836 |
| BHP / CML | -0.6025 |
-0.0638 |
-0.6044 |
-0.0643 |
| NCP / CML | 0.7999 |
0.1049 |
0.7471 |
0.1009 |
| BHP / Index | 2.3679 |
0.3009 |
2.3958 |
0.3035 |
| NCP / Index | 2.8325 |
0.4456 |
2.7357 |
0.4394 |
| CML / Index | 2.0308 |
0.3299 |
1.9313 |
0.3177 |
Table 2 : Covariances and Correlation Coefficients
As indicated by the correlation coefficients figures above, all combinations except BHP/CML are positively correlated. The BHP/CML pair is mildly negatively correlated at –0.0638, suggesting negative relationship of the direction of their return movement, but by only a small magnitude. NCP’s return is significantly correlated to the market movement at +0.4456, while BHP and CML have returns moving together with the market at +0.3009 and +0.3299 respectively.
3.3 Stocks and Market Analysis
Broken Hill Proprietary Limited:
BHP shares displayed a declining trend for the last 26 weeks. The price fell from $16.30 on 19th September 1997 to $15.65 on 13th March 1998. Despite the fact that prices do move up and down during the period from Dec 97 to Mar 98, the price eventually decreased to $15.65.
In mid Oct 97, the share prices dropped significantly from $15.08 to $14.11. This was caused by the lesser volume of trading between Australia and Asia due to the Asian financial crisis.
In Nov 97, the price continued to fall significantly to $13.80 partly due to investors turning their attention to Telstra after it was floated.
The share price continued to plunge 89 cents to $13.24. This was further aggravated by the sudden upset of the Tokyo share market.
By early February, BHP's share price recovered back to the $15.07 level. Many believe that the resignation announcement of BHP chief executive, John Prescott have a positive impact on its share prices which took a record high since Oct 97.
By the end of Feb 98, prices fell to $14.36 before it gradually picking up to $15.65 in Mar 98. This was assist by a number of call warrants being revived, which were rapidly being written off.
The News Corporation Limited:
From chart 1b, we can see that there has been a steady upward trend over the past 26 weeks on the stock prices for this firm, and presumable this industry. The stock prices closes at $6.31 on the 12 Sep 97 and closes at $9.91 on the 13 Mar 98.
There have not been any significant changes in the share prices over this period, except for some slight fluctuation. Shares prices in News Corporation soared to $8.47 on the New Year's Eve, its highest ever, after gaining $0.10 on the last trading day of the year. The company's preferred shares ended $0.124 stronger at $7.59, also a record close.
Market sentiment about the stock had been dampened in recent weeks by concerns about News Corporation's financial exposure to the $US200 million disaster movie and by ratings agency Standard & Poor's decision to downgrade NCP's credit rating to the lowest rank within the investment grade in early Dec 97.
Fortunately, reports from the US over the New Year, suggesting earlier fears about NCP’s US$135 million exposure to Titanic may now proved to be unfounded, and that the film may present a tidy profit to the NCP's Twentieth Century Fox studio and Viacom Inc's Paramount Studios.
Among the reasons cited for the increase in NCP's share price were surging earnings from the group's Fox Film and TV interests, the expiry of its liquid yield option notes and rumours that MSCI would not sell its preferred shares in the company.
Coles Myers:
There has not been pretty much ups and downs over the 26 weeks of sample period. However, the stock prices started off with $6.43 and finish off with $7.877. Similarly, the chart 1c also has an upward sloping trend as that of The News Corporations.
In the months of Sep and Oct 97, there had been an increase in the stock price for this industry. The abnormal gain from the property sales is accountable for this increase. There was an increase of 23.3% compared to the previous year, which had been inflated by a pre-tax profit of $44.6 million.
Coles Myers share prices has been trading at more than $7 since the start of Nov 97, up till Mar 98. The festive seasons of Christmas and the New Year, attributed to the improved sales figures. This was backed by the strong performance from the food and liquor divisions. As such, we would anticipate the share market to react positively to the active sales, whereby pushing the share prices on the 5 Dec 97 up to $7.48.
Since 16 Nov 97, the industry experiences a dampening share prices. Though not significant enough to create a commotion, it was believed that as a result of the Telstra float, consumers were tightening their expenses and altered their spending pattern. This would put a downward pressure on the sales figures.
Equally Weighted Portfolio as its name describes provide equivalent weightage on each return. Market performance is sometimes measured by an Equally Weighted Average of the return of each stock in an index. This technique which places equal weight on each return equates an implicit portfolio strategy that places equal dollar on each stock. As such, it differs from both Price weighting and Market Value weighting and also in terms of buy-and-hold portfolio strategies. This makes it an excellent benchmark for comparing investment performance. This is especially true when evaluating how investors with neither skill nor luck might perform.
4.1 Weighted Average Rate of Return
Equally weighted portfolio combines the three stocks together with equal weightage. The reason being it could help to diversify the risk, thereby decreasing the risk involved.
The equally weighted portfolio can be calculated using the variances of each stock and the covariances between them, with the help of matrix algebra. We can set the matrix as:

The portfolio variance as calculated is 3.6954% with a discrete rate of return of 0.8798% computed in Appendix 4. Note that the portfolio variances in Appendix 4 are similar with the matrix calculation.
The variance of equally weighted portfolio based on continuously compounded rate of return is calculated by:

4.2 Comparison between Equally Weighted Portfolio and
The risk-return of each individual stock and the equally weighted portfolio is presented in the table here:
Discrete Return |
Continuous Return |
|||||||
Return |
Variance |
Return |
Variance |
|||||
| BHP | -0.0271% |
12.0756% |
-0.0856% |
12.1987% |
||||
| NCP | 1.7942% |
7.8778% |
1.7418% |
7.5864% |
||||
| CML | 0.8725% |
7.3857% |
0.8339% |
7.2325% |
||||
| Equally Weighted Portfolio | 0.8798% |
3.6954% |
0.8300% |
3.6399% |
||||
Table 3 : Variances and Standard Deviations of Stocks and Equally Weighted Portfolio
As noted from the table above, the equally weighted portfolio has an average return (of the 3 individuals stocks) but bears the minimum risk indicated by its smallest variance. It illustrates the point that the risk of the portfolio will be lower than the highest risk share due to the diversification effect that occurs when assets are combined in a portfolio. The more assets in a portfolio, the more unsystematic risk that can be diversified away.
5. Markowitz Tangent Portfolio
There are several factors that must be taken into account when using the Markowitz Portfolio analysis. They are the risk, return and the degree of portfolio diversification of the stocks. The degree of portfolio diversification is dependent on the correlation among the individual asset returns. But first, we need to determine the proxy for the risk free rate.
5.1 Determining the Proxy for Risk-free rate
From the 90-day bank bill rates obtained over the 26 weeks period, we first convert the figures into weekly compounded rates by using the formula:
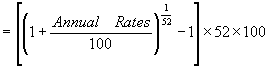
We then divide the weekly compounded rate by 52 (weeks) to get the weekly figures. The average of the weekly figures over the sample period gives the proxy for the risk free rate. As shown in Appendix 5, the proxy risk free rate is 0.09251%.
5.2 Weights of the Markowitz Tangent Portfolio
With the available returns, standard deviations and correlation coefficients of and between the selected 3 stocks, we can work out the weights of the Markowitz tangent portfolio. We first set the equation:
Ri - Rf = Z1s 1,i + Z2s 2,i + Z3s 3,i where i = BHP, NCP & CML.
Thus the equation for discrete returns is:
12.0756Z1 + 2.7621Z2 – 0.6025Z3 = -0.0271 – 0.09251
2.7621Z1 + 7.8778Z2 + 0.7999Z3 = 1.7942 – 0.09251
-0.6025Z1 + 0.7999Z2 + 7.3857Z3 = 0.8725 – 0.09251
Solving the equations simultaneously, we get:
Z1 = -0.0584
Z2 = 0.2288
Z3 = 0.0761 å (Z1, Z2, Z3) = 0.2465
Thus, their weights are:
WBHP = ![]() = -0.2369
= -0.2369
WNCP = 0.9282
WCML = 0.3087
With reference to the calculated figures on the weights of the three stocks, we determined that BHP has a weight of -0.2369, 0.9282 for NCP, and 0.3087 for CML. Based on economic interpretation, there are two reasons for assets to have negative weights. They may either be a short sale, or by issuing securities with same risk and return created a leverage portfolio.
Similarly, the weights for the Markowitz portfolio of the continuously compounded returns can be calculated by the following system:
12.1987Z1 + 2.7280Z2 – 0.6044Z3 = -0.0856 – 0.09251
2.7280Z1 + 7.5864Z2 + 0.7471Z3 = 1.7418 – 0.09251
-0.6044Z1 + 0.7471Z2 + 7.2325Z3 = 0.8339 – 0.09251
Solving the equations simultaneously, we get:
Z1 = -0.0627
Z2 = 0.2328
Z3 = 0.0732 å (Z1, Z2, Z3) = 0.2433
Thus, their weights are:
WBHP = ![]() = -0.2577
= -0.2577
WNCP = 0.9568
WCML = 0.3009
With the calculated weights, we can determine the variances by the formula:
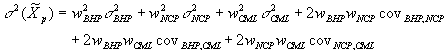
and the returns by:
![]() where i = BHP, NCP & CML
where i = BHP, NCP & CML
Calculating and compiling the risk-return figures into a table, we have:
Discrete Return |
Continuous Return |
||||||
Return |
Variance |
Return |
Variance |
||||
BHP |
-0.0271% |
12.0756% |
-0.0856% |
12.1987% |
|||
NCP |
1.7942% |
7.8778% |
1.7418% |
7.5864% |
|||
CML |
0.8725% |
7.3857% |
0.8339% |
7.2325% |
|||
Equally Weighted Portfolio |
0.8798% |
3.6954% |
0.8300% |
3.6399% |
|||
Markowitz Tangent Portfolio |
1.9411% |
7.5003% |
1.9395% |
7.5885% |
|||
Table 4 : Variances and Standard Deviations of Stocks and Portfolios
From the figures above, the returns for Markowitz tangent portfolio (for both discrete and continuously compounded returns) is the highest, much more than that of the equally weighted, while maintaining a smaller variance second only to the equally weighted portfolio’s and CML’s.
Representing these risk-return figures graphically, we have:
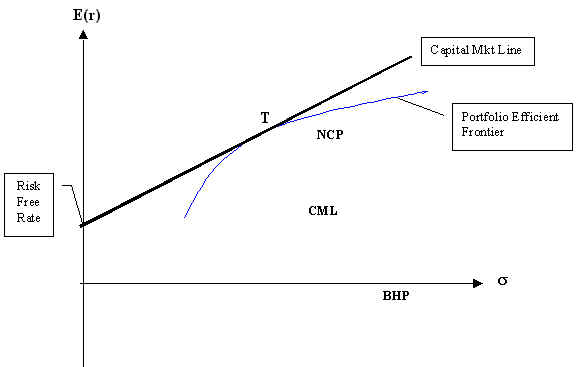
Figure 1 : The efficient portfolio frontier given the availability of a risk free asset
In Figure 1 above, the point of tangency between the capital market line and the portfolio frontier is the tangent portfolio, T. In this case, T is the Markowitz tangent portfolio calculated above to identify the optimal portfolio of the 3 selected assets, by finding the portfolio weights that result in the steepest capital asset line. The objective is to enable investors to mix the risk free asset with the optimal risky portfolio to achieve an optimal portfolio to satisfy a higher utility level. In order to secure a position either on or near the capital market line, it is essential to have the risk reducing power of diversification.
As shown in the diagram above, NCP lies closest to the efficient frontier where it represents a set of portfolios that maximise expected return at each level of portfolio risk. A risky stock will lie at a distance away from the frontier, and in this case BHP. With the correct weightage of combinations, the tangent portfolio at T allows investors to borrow or lend risk free asset to further satisfy their utility.
6. RISK
Total risk is divided into two parts - systematic risk and unsystematic risk. Systematic risk is non-diversifiable, and is attributable to market-wide risk sources. In contrast, unsystematic risk is a component of the total risk that can be eliminated by diversification. Both risks are estimated by the characteristic regression line of the stocks, which also states the stock systematic variability of return in terms of market forces that affect all stocks simultaneously. In this assignment, the total risk of the three stocks - BHP, NCP and CML, are measured by the variability of returns.
6.1 Systematic Risk & Unsystematic Risk
The fluctuation of stock prices, which leads to the reduction of risk, is all part of the nature of systematic risk. The proportion of systematic risk is given by:
= Systematic risk / Total risk
= b i2 Var (Rmt) / Var (Rit)
= Regression R2
= r 2 (Correlation Coefficient squared)
Beta (b ) is the measure of the systematic risk of a security. It is a tendency of a security’s returns to respond to swings in the broad market. If the beta is greater than 1, it means that the risk is high relative to the market. In contrast, the risk will be lower relatively to the market if beta is below 1. In addition, it is a standardise measure of its covariance with the market portfolio, as:
b i = Cov (Ri, Rm) / Var (Rm)
The slope of the regression line is b i. Cov (Ri, Rm) is the covariance of returns of each of the three stocks with the market calculated earlier, while
Cov (Rp, Rm) is calculated to be 2.4104. The variance of returns for the market portfolio, Var (Rm) = 5.1296 (discrete). Thus the calculated betas for BHP, NCP, CML and the equally weighted portfolio are 0.4616, 0.5522, 0.3959 and 0.4699 respectively (the beta of equally weighted portfolio can also be derived by taking the average of the 3 betas of each stock). The beta for NCP is the highest, but all stocks exhibit beta less than 1, suggesting that they are defensive assets. This indicates that they bear low market risk. The beta values relate directly to the firm’s nature of business, the capital structure of the firm, and the operating leverage of the firm. Any changes in the firm’s fundamentals may affect the beta value.
6.2 Partitioning the Total Risk
Given the calculated correlation coefficients between each stocks and the market, we can use this information to work out the systematic and unsystematic risk:
Thus, the partitioned risk components are given in the table below:
Discrete Return |
Continuous Return |
||||||
Systematic Risk |
Unsystematic Risk |
Systematic Risk |
Unsystematic Risk |
||||
BHP |
0.0905 |
0.9095 |
0.0921 |
0.9079 |
|||
NCP |
0.1986 |
0.8014 |
0.1931 |
0.8069 |
|||
CML |
0.1088 |
0.8912 |
0.1009 |
0.8991 |
|||
Equally Weighted Portfolio |
0.1326 |
0.8674 |
0.1287 |
0.8713 |
|||
Table 5 : Partition of total risk
As we have computed above, NCP has the greater fraction of return variability in the market movement. It has a higher R2 of 0.1986 (discrete), compared to BHP and CML with 0.0905 and 0.1088 respectively. The equally weighted portfolio has a systematic risk of 0.1326, which is the average risk of the 3 individual stocks. The same occurs for its unsystematic risk of 0.8674.
From the calculated risk components, we can say that BHP bears the lowest systematic risk, ie. the large proportion of non-market related is diversifiable by adding more stocks to form a more efficient portfolio. It is comforting to learn this as initially we saw that BHP is the riskiest stock among the 3 we have chosen. On the other hand, the more favourable NCP stock we have seen earlier bears the highest proportion of non-diversifiable risk, highlighting the firm’s risky nature. Thus the partition of risk to systematic and unsystematic risk help us gain an insight into the true risk nature of an investment.
As for the equally weighted portfolio, the fact that its risk components are the average of each risk, it illustrates that portfolio does help to reduce the risk of the riskiest stock within the portfolio at the expense of the less risky ones.
Graphically, the regression line represents the unsystematic risk. It can be eliminated by diversification to zero, hence, spreading the investment funds across the securities of firms whom operate independently. Systematic risk on the other hand is not diversifiable. Therefore, stocks with high systematic risk must be associated with high rates of return as an inducement for investors. The CAPM shows the relation between the stocks systematic risk and their expected rates of return.
Bodie Zvi, Kane Alex and Marcus Alan J. (1996) Investments, third ed., Irwin, USA
Harrington Diana R. (1987) Modern portfolio theory, The capital asset pricing
model & arbitrage pricing theory: A user’s guide, second ed.,
Prentice-Hall, USA
Brealey Richard A.and Myers Stewart C. (1996) Principles of corporate
Finance, fifth ed., McGraw-Hill, USA
Huntley Ian (1998) Shareholder – The handbook of Australian public
Company, 13th ed., The Australian Financial Review, Sydney
Various Authors (1997, 1998) The Australian Financial Review from Sep 97
till Mar 98.
8. Appendices [Click Here]